重み付けの抽選を行うアルゴリズム

こんにちは。プログラマーの尾関です。
今回は基本的なテクニックですが、知っておくと便利なアルゴリズムを紹介します。

例えば、くじを引いて以下のアイテムが手に入るとします。

• 10%で金のコイン
• 20%で銀のコイン
• 70%で銅のコイン

これをそのまま実装すると、以下のようなコードになると思います。

/**
 * コインの抽選を行う関数
 */
eItem LotCoin() {
  int rnd = rand()%100;
  if(0 <= rnd && rnd < 10) {
    // 10%で金のコイン
    return eItem_GoldCoin;
  }
  else if(10 <= rnd && rnd < 30) {
    // 20%で銀のコイン
    return eItem_SilverCoin;
  }
  else { // if(30 <= rnd && rnd < 100)
    // 70%で銅のコイン
    return eItem_CopperCoin;
  }
}

素直でわかりやすいコードですね。ただ、このやり方には2つの問題点があります。

1. 確率の合計が100になるようにしなければならない
2. 抽選する対象が増えると条件式が増える

最初の問題点は、例えば、銀のコインを30%と設定だけして、他の確率を減らすのを忘れた場合です。

• 10%で金のコイン
• 30%で銀のコイン
• 70%で銅のコイン

この指定では、合計した確率が110%となり、おかしな抽選が行われる可能性があります。例えば、先ほどの関数を通すと、銅のコインの出現確率が60%になってしまいます。つまり、データ入力をミスしたときに確率計算が意図しないものになる危険性があります。

もう1つの問題は、抽選対象が増えたときに、条件式が増えてしまうことです。例えば、レアアイテムとして「プラチナのコインが1%で出現する」という追加仕様が発生した場合、例としてあげた関数では、if文が増えることになってしまいます。

これらの問題点を回避するには、「重み付け」で抽選を行うようにします。考え方としては、以下のようなイメージです。抽選箱に、金のコインが1つ、銀のコインが2つ、銅のコインが7つ、入っていると考えます。

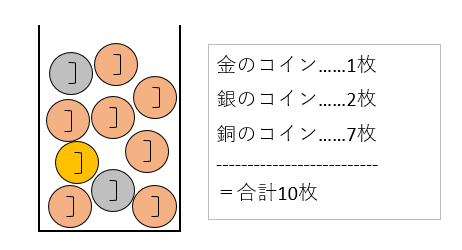
そして、抽選箱に入っているコインの合計枚数を求めます。

• コインの合計枚数 = 1 + 2 + 7 = 10

その合計値で、それぞれを割ることで、その結果、確率は同じものになります。

• 金のコイン： 1÷10＝10%
• 銀のコイン： 2÷10＝20%
• 銅のコイン： 7÷10＝70%

そして、条件式を減らすには、合計値から抽選した値を、各対象の重み(枚数)で減算して比較すると、for文で記述することができます。

int rnd = rand()%10; // 0～9
if(rnd < 1) {
  // 金のコイン
  return eItem_GoldCoin; // (0 <= rnd < 1)
}
rnd -= 1; // チェックが終わったので重みを減算

if(rnd < 2) {
  // 銀のコイン
  return eItem_SilverCoin; // (1 <= rnd < 3)
}
rnd -= 2; // チェックが終わったので重みを減算
if(rnd < 7) {
  return eItem_CopperCoin; // (3 <= rnd < 10)
}

わかりやすくするために、for文で書くべき記述を展開しています。
これを短くfor文で書いた処理は以下のとおりとなります。

/**
 * 重み付けで抽選を行う
 * @param pArray 抽選する対象の配列
 * @param Length 配列のサイズ
 */
int WeightedPick(int* pArray, int Length) {
  int totalWeight = 0;
  int pick = 0;

  // トータルの重みを計算する
  for(int i = 0; i < Length; i++) {
    totalWeight += pArray[i];
  }
  
  // 抽選する
  int rnd = rand()%totalWeight;

  for(int i = 0; i < Length; i++) {
    if(rnd < pArray[i]) {
      // 抽選対象決定
      pick = i;
      break;
    }
    
    // 次の対象を調べる
    rnd -= pArray[i];
  }
  
  return pick;
}

// 使用例
void main() {
  int Items[] = {1, 2, 7}; // 金:1  銀:2  銅:7
  // 抽選を行う (resultに抽選した対象の配列のインデックス番号が入る)
  int result = WeightedPick(Items, 3);
  
  const char* ItemNameTbl[] = {"Gold", "Silver", "Copper"};
  printf("抽選結果: %d", ItemNameTbl[result]);
}

この抽選を使った具体的な例として、趣味で作ったローグライクの入力データを紹介します。

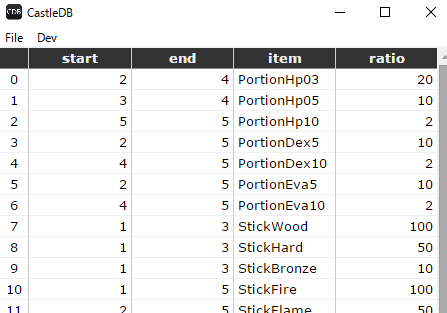
「ratio」という列が今回の話で言う「重み」にあたります。
StickWood(木の棒)と、StickFire(火の棒)のratioが、100になっているので、一番出現しやすいアイテムです。逆にPortionHp10(HPを10回復する薬)やPortionDex10(命中率を10%上昇させる薬)、PortionEva10(回避率を10%上昇させる薬)のratioは「2」となっているので、レアアイテムという位置づけです。

「start」「end」は出現するステージ番号です。startが1でendが3の場合、ステージ1～3でのみ出現するアイテムとなります。ローグライクはアイテムがランダムで出現しますが、序盤にいきなり強力なアイテムが手に入るとバランスが壊れてしまうので、序盤は弱い装備やアイテムを出現させるようにしています。

例えばステージ1では、以下の4つのアイテムが出現します。

• StickWood： 100
• StickHard： 50
• StickBronze： 10
• StickFire： 100

合計値は、100+50+10+100=260です。よって出現確率は以下の通りとなります。

• StickWood： 100÷260 = 38.46%
• StickHard： 50÷260 = 19.23%
• StickBronze： 10÷260 = 3.84%
• StickFire： 100÷260 = 38.46%

そしてステージ2へ進むと、別の装備やPortion系のアイテムが手に入るようになり、それらを含めた重み付けで抽選を行うようになります。

ということで、ローグライクのような抽選対象が増減するゲームでは、「重み付けの抽選」は非常に役に立つ、という話でした。

Follow me!